Download
Abstract
Clustering is an important tool in data analysis, with K-means being popular for its simplicity and versatility. However, it cannot handle non-linearly separable clusters. Kernel K-means addresses this limitation but requires a large kernel matrix, making it computationally and memory intensive. Prior work has accelerated Kernel K-means by formulating it using sparse linear algebra primitives and implementing it on a single GPU. However, that approach cannot run on datasets with more than approximately 80,000 samples due to limited GPU memory. In this work, we address this issue by presenting a suite of distributed-memory parallel algorithms for large-scale Kernel K-means clustering on multi-GPU systems. Our approach maps the most computationally expensive components of Kernel K-means onto communication-efficient distributed linear algebra primitives uniquely tailored for Kernel K-means, enabling highly scalable implementations that efficiently cluster million-scale datasets. Central to our work is the design of partitioning schemes that enable communication-efficient composition of the linear algebra primitives that appear in Kernel K-means. Our 1.5D algorithm consistently achieves the highest performance, enabling Kernel K-means to scale to data one to two orders of magnitude larger than previously practical. On 256 GPUs, it achieves a geometric mean weak scaling efficiency of 79.7% and a geometric mean strong scaling speedup of 4.2×. Compared to our 1D algorithm, the 1.5D approach achieves up to a 3.6× speedup on 256 GPUs and reduces clustering time from over an hour to under two seconds relative to a single-GPU sliding window implementation. Our results show that distributed algorithms designed with application-specific linear algebraic formulations can achieve substantial performance improvement.
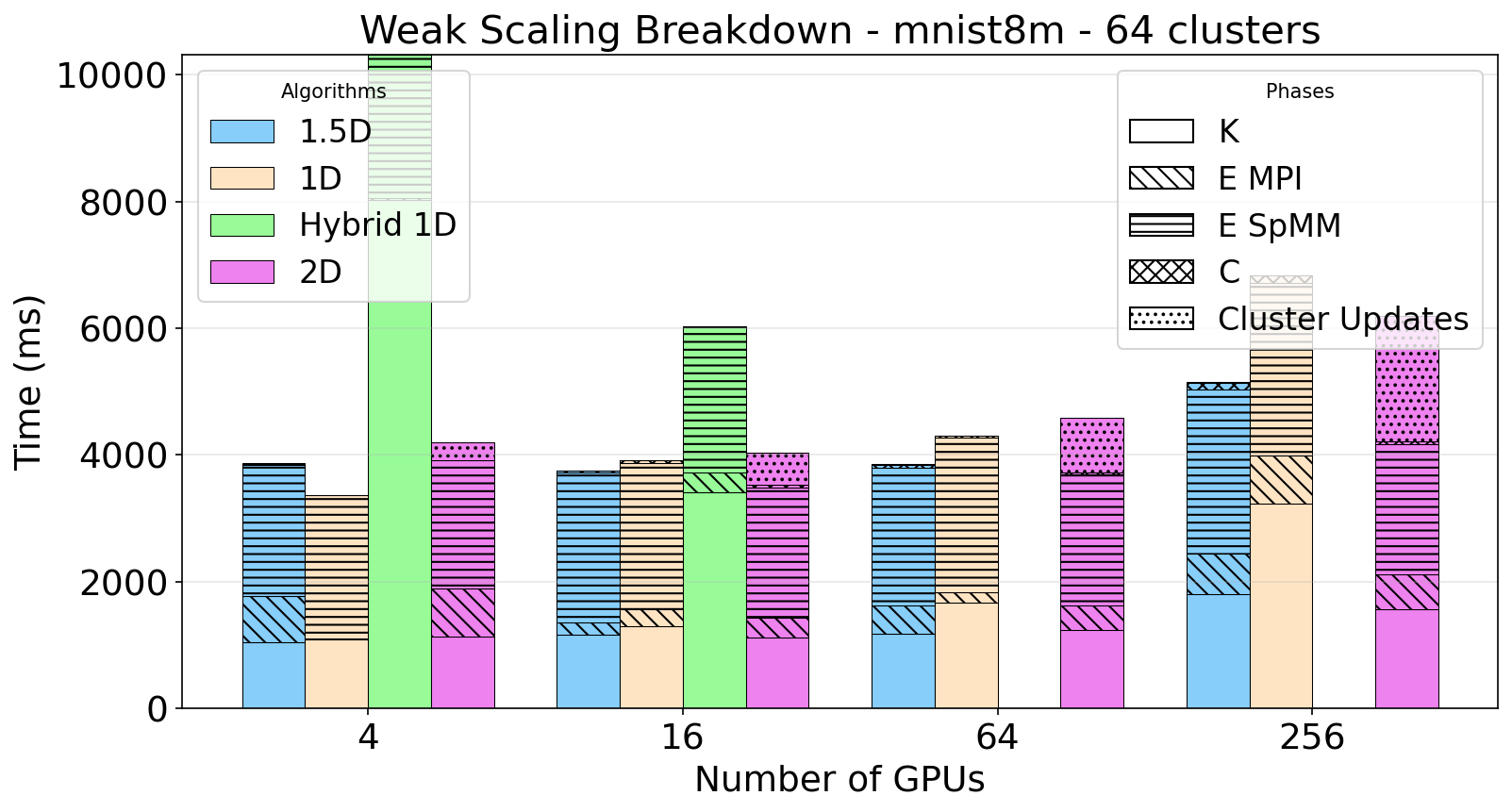
Figure 3: Weak Scaling (MNIST 8m)
Citation
Julian Bellavita, Matthew Rubino, Nakul Iyer, Andrew Chang, Aditya Devarakonda, Flavio Vella and Giulia Guidi. 2026. “Communication-Avoiding Linear Algebraic Kernel K-Means on GPUs” arXiv:2601.17136. https://arxiv.org/abs/2601.17136 (Accepted, IPDPS'26).
@misc{bellavita2026communicationavoidinglinearalgebraickernel,
title={Communication-Avoiding Linear Algebraic Kernel K-Means on GPUs},
author={Julian Bellavita and Matthew Rubino and Nakul Iyer and Andrew Chang and Aditya Devarakonda and Flavio Vella and Giulia Guidi},
year={2026},
eprint={2601.17136},
archivePrefix={arXiv},
primaryClass={cs.DC},
url={https://arxiv.org/abs/2601.17136},
}